1 Minute Tips

日: 2019年1月27日

  • 行列演算の基礎

    行列演算の基礎

    はじめに

    重回帰分析をするにあたり必要な計算があるので整理する。

    • ベクトルの定義
    • 行列の定義
    • 転置
    • 逆行列
    • 行列積

    numpyはimportされているものとする

    import numpy as np

    ベクトルの定義

    #  ベクトルの定義
x = np.array([[1],[2],[3]])
print(x)

    行列の定義

    X = np.array([[1,2],[3,4]])
print(X)

     

    転置

    # 転置
Xt = X.T
print(Xt)

    逆行列  

    linear algebra　（リニア・アルジェブラ）線形代数の意味 
    Inverse （インバース）　逆行列の意味

    X_inv = np.linalg.inv(X)
print(X_inv)

    行列積

    XX_inv = np.dot(X,X_inv)
print(XX_inv)

    10
    8.88の16乗1

    x掛けるxの逆行列で行列積が求まる。

    よく使う計算

    以下の様なnumpyの配列を作り、行、列の数を取得したり、forループで値を取得したりする

    import numpy as np
x = np.array([[1,2,3]])
print (x)
print ('-----')

X = np.array([[1,2],[3,4]])
row, cal = X.shape

print(row)
print(cal)
print ('-----')

for x in X:
    print ('-----')
    print (x)
~                                                                                       
~

    実行結果

    $ python sample.py
[[1 2 3]]
-----
2
2
-----
-----
[1 2]
-----
[3 4]

     

    演習

    xとyを以下の通り定義する。xの1行目にはダミー値として1をセットする事。

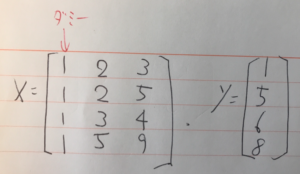
    # X definitions
print('# X definitions')
X = np.array([
    [1,2,3],
    [1,2,5],
    [1,3,4],
    [1,5,9]
])

print(X)

# Y definitions
print('# Y definitions')
y = np.array([
  [1],
  [5],
  [6],
  [8]
])

print(y)

    実行結果

    # X definitions
[[1 2 3]
 [1 2 5]
 [1 3 4]
 [1 5 9]]
# Y definitions
[[1]
 [5]
 [6]
 [8]]

    また、wは以下の通りとし、stepを分けて計算する

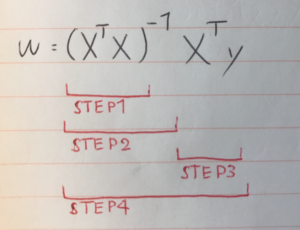
    # Step1
print('# Step1')
step1 = np.dot(X.T, X)
print(step1)

# Step2
print('# Step2')
step2 = np.linalg.inv(step1)
print(step2)

# Step3
print('# Step3')
step3 = np.dot(X.T,y)
print(step3)

# Step4
print('# Step4')
step3 = np.dot(X.T,y)
step4 = np.dot(step2,step3)
print (step4)

    実行結果は以下の通り

    # Step1
[[  4  12  21]
 [ 12  42  73]
 [ 21  73 131]]
# Step2
[[ 1.76530612 -0.39795918 -0.06122449]
 [-0.39795918  0.84693878 -0.40816327]
 [-0.06122449 -0.40816327  0.24489796]]
# Step3
[[ 20]
 [ 70]
 [124]]
# Step4
[[-0.14285714]
 [ 0.71428571]
 [ 0.57142857]]