はじめに
重回帰分析を進めるにあたりスカラー、ベクトル、行列を整理。ベクトルと行列の足し算・引き算についてまとめた。
スカラー
“` x, y, z, M, N “`
数学に出てくる記号
ベクトル
複数の定数、複数の変数を集めたもの。
スカラーが複数個集まれば、ベクトルになる。
教科書やノートではベクトルのxはスカラーのxと混乱するのを防ぐべく、太文字で書くのが一般的。
エクセルのカラムをイメージするとよい
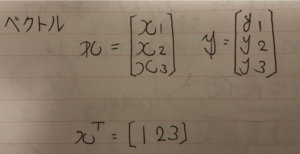
横向きにする事も可能。
その場合は転置の記号(T)を付ける
行列
ベクトルに対して横方向を持ったもの
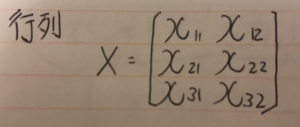
この場合は、3 * 2の行列
行列の演算(足し算・引き算)について
対応するところを合わせる
足し算の場合
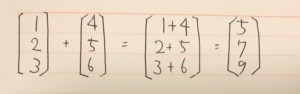
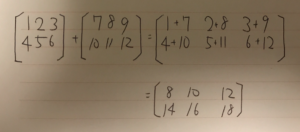
引き算の場合
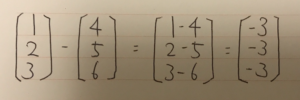
条件
計算するベクトルの行と列の数が同じである事
行列の演算(掛け算)について
基本的に行列の割り算はない。分数をかける事により掛け算のみで代用できるため。
行列は対応するところを計算するわけではない。
例えばこのような行列があった場合
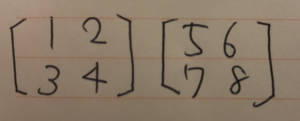
縦、横に補助線を引く
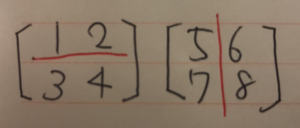
左側と右側を掛ける。
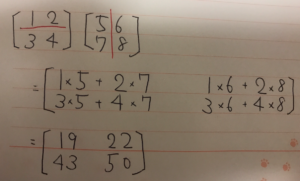
条件
足し算・引き算とは違い、サイズが同じでなくても良い。
内側の2つが同じである事。
“`N… Aの行
M… Aの列
O… Bの行
P… Bの列 “`
だとすると
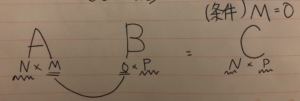
AとBの行列を掛ける場合、
M=Oが一致している事。
また、算出されるCの行と列の数はN・Pになる
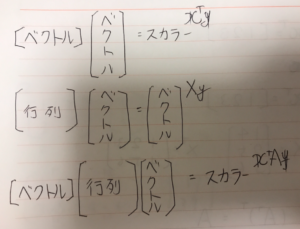
ベクトル・行列を掛けるとどうなるか
転置の公式
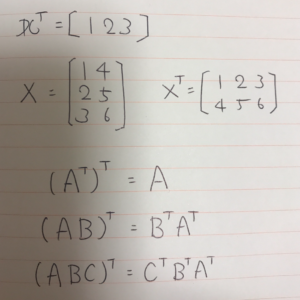
ベクトルで微分の公式

最後に
本記事はキカガクさんの Udemyで勉強したノートになります。
あくまでも私のノートになりますので詳しく知りたい方はキカガクさんのコースを受講してみてください
https://www.udemy.com/kikagaku_blackbox_2

